RELATIONS, FUNCTIONS, GRAPHS

​

You should be able to

 explain concepts associated with relations;

 

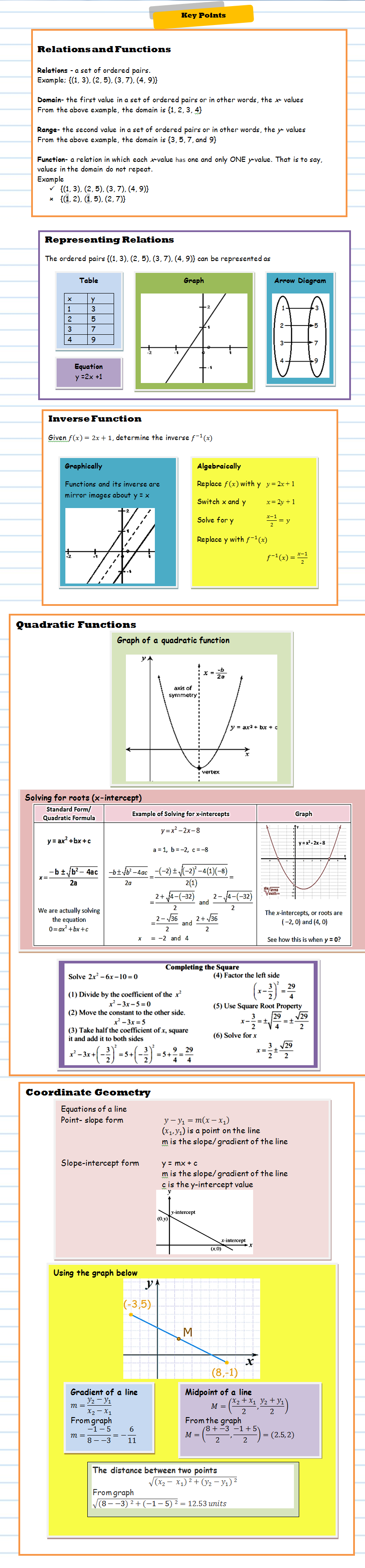
Concept of a relation, types of relation, examples and non-examples of relations, domain, range, image, co-domain.

 

 represent a relation in various ways;

 

Set of ordered pairs, arrow diagrams, graphically, algebraically.

 state the characteristics that define a function;

 

Concept of a function, examples and non-examples of functions.

 use functional notation;

 

 

 distinguish between a relation and a function;

 

Ordered pairs, arrow diagram, graphically (vertical line test).

 draw and interpret graphs of linear functions;

 

Concept of linear function, types of linear function (y = c; x = k; y = mx + c; where m, c and k are real numbers).

 determine the intercepts of the graph of linear functions;

 

x-intercepts and y-intercepts, graphically and algebraically.

 determine the gradient of a straight line;

 

Concept of slope.

 

 determine the equation of a straight line;

 

The graph of the line. The co-ordinates of two points on the line. The gradient and one point on the line. One point on the line and its relationship to another line.

 solve problems involving the gradient of parallel and perpendicular lines;

 

 determine from co-ordinates on a line segment:

(a) the length; (b) the co-ordinates of the midpoint;

The concept of magnitude or length, concept of midpoint.

 

 solve graphically a system of two linear equations in two variables;

 

 represent the solution of linear inequalities in one variable using:

(a) set notation;

(b) the number line;

(c) graph;

 

 draw a graph to represent a linear inequality in two variables;

 

 use linear programming techniques to solve problems involving two variables;

  

 derive composite functions;

 

Composite function, for example, fg, f2 given f and g. Non-commutativity of composite functions (fg≠gf).

 state the relationship between a function and its inverse;

 

The concept of the inverse of a function.

 derive the inverse of a function;

f-1, (fg)-1

 evaluate f(a), f-1(a), fg(a), (fg)-1(a);

 

 use the relationship (fg)-1= g-1 f-1;

The concept of the inverse of a function, determining the inverse of a given function.

 

 draw and interpret graphs of a quadratic function to determine:

(a) the elements of the domain that have a given image;

(b) the image of a given element in the domain;

(c) the maximum or minimum value of the function;

(d) the equation of the axis of symmetry;

(e) the interval of the domain for which the elements of the range may be greater than or less than a given point;

(f) an estimate of the value of the gradient at a given point;

(g) intercepts of the function;

 

 determine the axis of symmetry, maximum or minimum value of a quadratic function expressed in the

form a(x + h)2 + k;

 

 sketch graph of quadratic function expressed in the form a(x+h)2 + k and determine number of roots;

 

 draw and interpret the graphs of other non-linear functions;

 

y=axn where n = -1,-2 and +3.

 

 draw and interpret distance-time graphs and speed-time graphs (straight line only) to determine:

 

(a) distance;

(b) time;

(c) speed;

(d) magnitude of acceleration.